Thursday, November 13, 2014
Ping-Pong Valence Sphere Model
Valence sphere models, a qualitative chemical bond model that includes the influence of the electron pair repulsion among valence electron pairs and attraction between positive atomic core and negative electron pairs, can be constructed with Ping-Pong balls easily. Here, I made three pairs of linked ping-pong balls and used them to create a tetrahedral sp3-hybridized AX4 system and a octahedral d2sp3 hybridized AX6 system.
Wednesday, November 12, 2014
Beautiful photo of Chern's C60@60 at the Columbia Secondary School
The superbuckyball, C60@C60, made by Chern is now on exhibition at the Columbia Secondary School, New York.
This is for an event
called MoSAIC—Mathematics of Science, Art, Industry, Culture—the festival, an offshoot of the annual Bridges Organization international conference dedicated to the connections between art and mathematics.
There is a nice photo of this C60@C60 in the Columbia Spectator.

There is a nice photo of this C60@C60 in the Columbia Spectator.

Thursday, November 6, 2014
Bead model of Klein's all-heptagon network
I took a picture of single tetrahedral unit (12 heptagons) of D56 bead model on the figure
depicting schematically an open network consisting only of heptagons, described by Klein in his 1879 paper.
Klein, F. (1878). "Ueber die Transformation siebenter Ordnung der elliptischen Functionen" [On the order-seven transformation of elliptic functions]. Mathematische Annalen 14 (3): 428–471. Translated in Levy, Silvio, ed. (1999). The Eightfold Way. Cambridge University Press.
Klein, F. (1878). "Ueber die Transformation siebenter Ordnung der elliptischen Functionen" [On the order-seven transformation of elliptic functions]. Mathematische Annalen 14 (3): 428–471. Translated in Levy, Silvio, ed. (1999). The Eightfold Way. Cambridge University Press.
Thursday, October 23, 2014
Evolution of superbuckyballs
Since the last month of 2011, I started to work on the so-called Sierpinski buckyballs or superbuckyballs, which belong to a particular family of fullerenes created by treating C60s as supernodes and carbon nanotubes as superbonds. Using this idea, an unlimited number of hierarchical super-structures of sp2-hybridized (3-coordinated) carbons can be constructed. Before this task was really started, I have managed to build some simpler structures such as super-triangle, super-tetrahedron, and other related structures. With the experience, I firmly believed in the feasibility of creating bead models of much larger superbuckyballs.
But
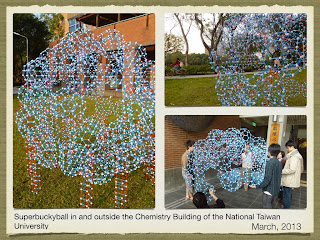
it is too tedious to construct bead models for this kind of super-structures, especially the so-called C60xC60, alone. So I designed a modular approach to build these models collaboratively. I told a few chemistry teachers, especially Dr. Chou (周芳妃), at a local high school, The Taipei First-Girl School (TFGH), about this structure. They were glad to try this idea out together. The results are two beautiful superbuckyballs (or C60xC60) made by 6mm and 12 mm beads, respectively. Both of the structures were on public display for the anniversary of TFGH and a simultaneous event of the TFGH's 30-year alumni reunion. Alumni association of TFGH kindly supported the whole project. Dr. Tsoo was one of alumni that year, that was why we got supported from them.
Later on, I made another bead model of C60xC60 for the JMM held in San Diego about two years ago (Jan. 2013). I used the photo of the giant bead model students and I made in the JMM description though.
I met Chern (莊宸) in the meeting. We discussed the structural rules for this family of compounds. Particularly, I commented on that the particular model I made cannot be constructed by Zometool. After returning back to Cambridge, MA, Chern solved the problem by carefully puncturing holes along certain symmetry axes in order to be consistent with the Zometool requirements.
Yuan-Jian Fan (范原嘉) then proved Chern's idea by building a virtual C60xC60 super-buckyball with the zometool construction software, vZome, which was kindly given to us by its author, Scott Vorthmann, a few years ago. With everything ready, a few enthusiastic students from the theoretical chemistry group of the National Taiwan University started to build the first zometool super buckyball after the Chinese new year.
Soon, a number of practical issues on the construction of a real zometool model of C60xC60 super-buckyball appeared. The first issue is the structural stability against gravity. The original neck structures (shortest situations) designed by Chern consisted of a number of octagons were too weak and simply cannot hold the whole structure due to its own weight. Another issue is still weight, without extra stands, the southern hemisphere of super-buckyball constructed by zometool simply cannot hold the northern hemisphere. Finally, how to put those parts on top without scaffold is also a question. All these problems were solved beautifully by Yuan-Jia Fan. Of course, local dealer, Helen Yu, of Zometool in Taiwan is also helpful. She always responded us with the necessary zometool pieces upon our requests in a very short time. So, we can have the first zometool sculpture of C60xC60 erected in the NTU campus around mid-March. Chern then proposed to Paul Hildebrand to have a family-day activity for the 2013 Bridges which will be held in Enschede that year. Paul agreed to provide us with the necessary materials. At the family day, we got more help from a few Bridges participants and their family members from Taiwan. These included Profs. Liu (劉柏宏) and Tung-Shyan Chen (陳東賢). Without them the final C60xC60 structure couldn't be finished in such a short period. In addition to the construction of huge zometool superbuckyball, Chern also presented a small bead model to the Bridges meeting as shown in the following pictures based on the same construction rule he designed. Another bead model in his right hand is an edge-elevated dodecahedron assembled from fifty C80s, twenty for the vertices of dodecahedron and thirty for the elevated edges. The idea for making this one is similar to C60xC60. I brought them back to Taiwan and put them on exhibition in the NTU Chemistry Museum for about a year until the last July when Chern got an email from George Hart asking him about the possibility of donating this small C60xC60 model for MoSAIC (Mathematics of Science, Art, Industry, and Culture) traveling exhibition. In the email, George commented on this model as " having the right combination of artistic expression, mathematical content, and practical transportability".
Soon, a number of practical issues on the construction of a real zometool model of C60xC60 super-buckyball appeared. The first issue is the structural stability against gravity. The original neck structures (shortest situations) designed by Chern consisted of a number of octagons were too weak and simply cannot hold the whole structure due to its own weight. Another issue is still weight, without extra stands, the southern hemisphere of super-buckyball constructed by zometool simply cannot hold the northern hemisphere. Finally, how to put those parts on top without scaffold is also a question. All these problems were solved beautifully by Yuan-Jia Fan. Of course, local dealer, Helen Yu, of Zometool in Taiwan is also helpful. She always responded us with the necessary zometool pieces upon our requests in a very short time. So, we can have the first zometool sculpture of C60xC60 erected in the NTU campus around mid-March. Chern then proposed to Paul Hildebrand to have a family-day activity for the 2013 Bridges which will be held in Enschede that year. Paul agreed to provide us with the necessary materials. At the family day, we got more help from a few Bridges participants and their family members from Taiwan. These included Profs. Liu (劉柏宏) and Tung-Shyan Chen (陳東賢). Without them the final C60xC60 structure couldn't be finished in such a short period. In addition to the construction of huge zometool superbuckyball, Chern also presented a small bead model to the Bridges meeting as shown in the following pictures based on the same construction rule he designed. Another bead model in his right hand is an edge-elevated dodecahedron assembled from fifty C80s, twenty for the vertices of dodecahedron and thirty for the elevated edges. The idea for making this one is similar to C60xC60. I brought them back to Taiwan and put them on exhibition in the NTU Chemistry Museum for about a year until the last July when Chern got an email from George Hart asking him about the possibility of donating this small C60xC60 model for MoSAIC (Mathematics of Science, Art, Industry, and Culture) traveling exhibition. In the email, George commented on this model as " having the right combination of artistic expression, mathematical content, and practical transportability".
Wednesday, October 22, 2014
Tuesday, October 21, 2014
Da Vinci's elevated polyhedra
Leonardo da Vinci (1452-1519) made outstanding illustrations for Luca Pacioli's 1509 book "The Divine Proportion", in which they described "elevated" forms of many polyhedra. In the Seoul Bridges meeting this year, Rinus Roelofs presented a beautiful paper on the similarities and differences between Da Vinci's elevations and Kepler's stellations.
For details, check the following pdf file:
Rinus Roelofs, Elevations and Stellations, Proceedings of Bridges 2014: Mathematics, Music, Art, Architecture, Culture, 235-242.
Figure 1 and 2 in the paper are original illustrations made by Leonardo da Vinci:
It is interesting that bead models for the five elevated regular polyhedra can be built easily with great effects. Among them, elevated cube and dodecahedron are more flexible as expected.
Also, these five elevated Platonic solids can be viewed as nonconvex deltahedra with the names, triakis tetrahedron, tetrakis hexahedron, triakis octahedron (stella octangula), pentakis dodecahedron, and triakis icosahedron, respectively.
Additionally, the elevated icosidodecahedron was also illustrated beautifully by Da Vinci in the book.
The corresponding bead model can also be built!
For details, check the following pdf file:
Rinus Roelofs, Elevations and Stellations, Proceedings of Bridges 2014: Mathematics, Music, Art, Architecture, Culture, 235-242.
Figure 1 and 2 in the paper are original illustrations made by Leonardo da Vinci:
It is interesting that bead models for the five elevated regular polyhedra can be built easily with great effects. Among them, elevated cube and dodecahedron are more flexible as expected.
Also, these five elevated Platonic solids can be viewed as nonconvex deltahedra with the names, triakis tetrahedron, tetrakis hexahedron, triakis octahedron (stella octangula), pentakis dodecahedron, and triakis icosahedron, respectively.
Additionally, the elevated icosidodecahedron was also illustrated beautifully by Da Vinci in the book.
The corresponding bead model can also be built!
Sunday, October 19, 2014
Saturday, October 18, 2014
One more Truss model of perovskite (or fluorite/antifluorite) structure
I made another truss model of perovskite structure with octahedra constructed by yellow and blue bugle beads.
Sunday, October 12, 2014
Friday, October 10, 2014
Monday, September 29, 2014
Truss models of cubic and hexagonal closest packings
I made two more bead models of two-layer cuboctahedron and twisted cuboctahedron (anticuboctahedron) to illustrate the vector equilibrium of Buckminster Fuller.
Through these two models, the connection to the cubic and hexagonal closest packings can also be visualized more easily.
Sunday, September 28, 2014
Two icosahedral complexes derived from an icosahedron
Starting from a bead model of icosahedron, one can make a few beautiful rigid polyhedral complexes by adding more regular octahedra and tetrahedra surrounding the central icosahedron. Here are two examples:
Icosahedron + Icosidodecahedron
Icosahedron + Icosidodecahedron + Rhombic Hexecontahedron
Icosahedron + Icosidodecahedron
Icosahedron + Icosidodecahedron + Rhombic Hexecontahedron
Wednesday, August 13, 2014
Four bead models for the Bridges 2014 Seoul
The very first day of Bridges 2014 for setting up the mathart exhibit:
Horibe, Chia-Chin and I are going to have workshop, From Sangaku Problems to Mathematical Beading: A Hands-on Workshop..., for this meeting this afternoon.
Horibe, Chia-Chin and I are going to have workshop, From Sangaku Problems to Mathematical Beading: A Hands-on Workshop..., for this meeting this afternoon.
Wednesday, July 30, 2014
Workshop at BCCE, Grand Valley State Univ.
I will give one more workshop in the 2014 Biennial Conference on Chemical Education
which is hosted by the Grand Valley State Univ, Michigan next week.
My workshop is arranged in the afternoon (2:00-5:00PM) of Aug. 4.
It is free. Hopefully, I brought enough beads with me for every participant.
Saturday, July 26, 2014
"Mathematicians Solve The Topological Mystery Behind The “Brazuca” World Cup Football Just in time for the World Cup final"
I just noticed that there is a page from Medium - Everyone’s stories and ideas,
Mathematicians Solve The Topological Mystery Behind The “Brazuca” World Cup Football Just in time for the World Cup final,
which reported the manuscript, From the "Brazuca" ball to Octahedral Fullerenes: Their Construction and Classification, Yuan-Chia Fan and I submitted to the arXiv at the end of last month.
In fact, Yuan-Jia has been working on the general structural rules for this peculiar family of generalized fullerenes with octahedral symmetry for a period of time. When the FIFA World Cup started in the mid June, I noticed quite accidentally that the official soccer ball, the “Brazuca”, for the FIFA World Cup held in Brazil this year has exactly the same octahedral symmetry. Then, we rewrote the draft a little bit and changed the title to its current form. However, the manuscript was first rejected by the Journal of Chemical Information and Modelling because the paper is not of general interest to the readers of the journal. And then it was rejected again by the Journal Physical Chemistry A because the editor thought this paper falls outside the bounds of the journal.
Instead of finding another journal, I decided to put it in the print archive, arXiv, at the end of June. So people might find it interesting during the World Cup season.
The evolution of the official Adidas Soccer Balls since 1970.
In addition to the page on Medium - Everyone’s stories and ideas, I also noticed three more pages which refer to the Yuan-Jia's work on the octahedral fullerenes and their connection to the Brazuca:
Mathematicians Solve The Topological Mystery Behind The “Brazuca” World Cup Football Just in time for the World Cup final,
which reported the manuscript, From the "Brazuca" ball to Octahedral Fullerenes: Their Construction and Classification, Yuan-Chia Fan and I submitted to the arXiv at the end of last month.
In fact, Yuan-Jia has been working on the general structural rules for this peculiar family of generalized fullerenes with octahedral symmetry for a period of time. When the FIFA World Cup started in the mid June, I noticed quite accidentally that the official soccer ball, the “Brazuca”, for the FIFA World Cup held in Brazil this year has exactly the same octahedral symmetry. Then, we rewrote the draft a little bit and changed the title to its current form. However, the manuscript was first rejected by the Journal of Chemical Information and Modelling because the paper is not of general interest to the readers of the journal. And then it was rejected again by the Journal Physical Chemistry A because the editor thought this paper falls outside the bounds of the journal.
Instead of finding another journal, I decided to put it in the print archive, arXiv, at the end of June. So people might find it interesting during the World Cup season.
The evolution of the official Adidas Soccer Balls since 1970.
In addition to the page on Medium - Everyone’s stories and ideas, I also noticed three more pages which refer to the Yuan-Jia's work on the octahedral fullerenes and their connection to the Brazuca:
Thursday, July 10, 2014
Workshop for the NTU CampCamp
The first few slides and a few photos from the workshop I had for the NTU ChemCamp this afternoon in the Chemistry Building of National Taiwan University:
Wednesday, July 9, 2014
First slides for my talk in Center for Synchrotron Radiation and workshop for the Chemcamp
I have two opportunities to talk about the mathematical beading this month. The first one was given to people working at the Center of Synchrotron Radiation on Jul. 1. The first slide of the talk is given here:
Tomorrow I will give a 40-min talk before the hands-on workshop for about 30 high-school students who participate the Chemcamp these few days. The first slide of the talk is given as follows.
Tomorrow I will give a 40-min talk before the hands-on workshop for about 30 high-school students who participate the Chemcamp these few days. The first slide of the talk is given as follows.
Another two workshops in this summer
In addition to the workshop in Seoul, Korea for the Bridges conference,
I will give two more workshops in this summer: the first one is for the Chemistry Camp in the chemistry building (積學館) of the National Taiwan University this Thursday (1:30PM-5:00PM, Jul. 10, 2014) and another one for the 2014 Biennial Conference on Chemical Education (BCCE, Aug. 3-7, 2014) which will be held in the Grand Valley State University (Michigan, USA). My workshop in BCCE is on Aug. 4, 2014.
Tuesday, July 8, 2014
The weight of mathematics
Is there a weight for a mathematical problem? The answer is Yes, if you talk about the Sangaku problem from the Edo period of Japan. Under the kind arrangement of Prof. Sonoda and Mr. Horibe during my visit to Nagoya this May (May 11, 2014), I was fortunate enough to see a few wooden Sangaku tablets, replica and original one, and really saw that mathematical problems can be really heavy. The next day after Horibe-San gave a workshop, Dr. Fukugawa Hidetoshi and I gave the other two talks in the Nagoya City University, we visited two temples in the Nagoya area.
Dr. Fukagawa is the premier authority on the Sangaku tablets in Japan. But he had a serious cold in that weekend, but still insisted to go with us to visit these places. In addition to him and me, we were also jointed with Mr. Horibe, Prof. Sonoda, one local high school math teacher to see these Sangaku wooden tablets.
The first temple we went is the Atsuta Shrine(Atsuta Jingu/熱田神宮). Right after we arrived, we were guided to a special room in the second floor by people from the Shrine, where the replica of two Sangaku tablets (dated 1841 and 1844, respectively) are carefully stored and not on display usually. Because we were special guests of Dr. Fukagawa, so we were lucky enough to have the privilege to examine these two beautifully-made replica.
After we had a brief lunch at Atsuta Shrine, Mr. Horibe brought us to a beautiful temple, Yourinzi temple (明星輪寺), in a nearby mountain area, Mount Ikeda (Ikeda-yama, 金生山) of Ogaki city, Gifu prefecture (岐阜縣大垣市). In this Buddhist temple, there is a well preserved Sangaku tablet made in 1865. Most importantly, many mathematicians and physicists, including Freeman Dyson, have been invited by Dr. Fukagawa to visit this temple to see the Sangaku tablet before.
Dr. Fukagawa is the premier authority on the Sangaku tablets in Japan. But he had a serious cold in that weekend, but still insisted to go with us to visit these places. In addition to him and me, we were also jointed with Mr. Horibe, Prof. Sonoda, one local high school math teacher to see these Sangaku wooden tablets.
The first temple we went is the Atsuta Shrine(Atsuta Jingu/熱田神宮). Right after we arrived, we were guided to a special room in the second floor by people from the Shrine, where the replica of two Sangaku tablets (dated 1841 and 1844, respectively) are carefully stored and not on display usually. Because we were special guests of Dr. Fukagawa, so we were lucky enough to have the privilege to examine these two beautifully-made replica.
After we had a brief lunch at Atsuta Shrine, Mr. Horibe brought us to a beautiful temple, Yourinzi temple (明星輪寺), in a nearby mountain area, Mount Ikeda (Ikeda-yama, 金生山) of Ogaki city, Gifu prefecture (岐阜縣大垣市). In this Buddhist temple, there is a well preserved Sangaku tablet made in 1865. Most importantly, many mathematicians and physicists, including Freeman Dyson, have been invited by Dr. Fukagawa to visit this temple to see the Sangaku tablet before.
Subscribe to:
Posts (Atom)