I got a very nice catalog for the 2012 Exhibition of Mathematical art of JMM from Chern today. Here are two pictures, one for the cover page and the next one for our beadworks on TPMS.
Thursday, June 28, 2012
Saturday, June 23, 2012
Twistane
Monday, June 18, 2012
Dendritic structures
Mr. Horibe made a number of dendritic fullerenes which are similar to the Kepler's stellated polyhedrons. By using the Euler theorem, it is quite straightforward to show that, in a cage-like fullerene without hole, N5-N7=12, where N5 and N7 are the number of pentagons and heptagons, respectively. In the typical fullerenes where the local Gaussian curvature is positive everywhere, we should have N7=0. The total number of pentagons is 12. Another way to put it is to introduce the so-called topological charge, 1 for a pentagon and -1 for a heptagon. So the topological charge of a cage-like fullerene is 12.
Heptagons always generate a negative Gaussian curvature. For a cage-like fullerene, whenever we introduce an extra heptagon, we have to include a pentagon in order to satisfy the identity N5-N7=12.
One can replace a pentagon in a Goldberg icosahedron (icosahedral fullerene) by 6 pentagons (a hemisphere of C20) and 5 heptagons to get a spike. So the topological for this area is still 1 after replacement. Similarly, we can do the same replacement for all other 11 pentagons to get a dendritic structure.

Of course, we can use the same kind of trick to "grow" a spike (a carbon nanotube endcapped with the hemisphere of a C20) along the normal direction of any pentagon on any kind of graphitic structure.
Incidentally, this structure without the C20 caps is just the inner part of the high-genus fullerenes we have done before.

Heptagons always generate a negative Gaussian curvature. For a cage-like fullerene, whenever we introduce an extra heptagon, we have to include a pentagon in order to satisfy the identity N5-N7=12.
One can replace a pentagon in a Goldberg icosahedron (icosahedral fullerene) by 6 pentagons (a hemisphere of C20) and 5 heptagons to get a spike. So the topological for this area is still 1 after replacement. Similarly, we can do the same replacement for all other 11 pentagons to get a dendritic structure.

Of course, we can use the same kind of trick to "grow" a spike (a carbon nanotube endcapped with the hemisphere of a C20) along the normal direction of any pentagon on any kind of graphitic structure.
Incidentally, this structure without the C20 caps is just the inner part of the high-genus fullerenes we have done before.

Friday, June 15, 2012
Workshop in the Hakozaki campus of Kyushu University
I gave a workshop in the chemistry department located at the Hakozaki campus of Kyushu University on Jun. 5, 2012. The workshop was hosted by Prof. Teruo Shinmyozu.
Since participants are undergraduate, graduate students and some faculty members of Kyushu univ., so I gave some more details about the chemistry of molecular beading. Particularly, I talked about that the connection between beads and valence electron pairs. Bead models of molecules are possibly the only physical models that take advantage of the analogy between microscopic interactions and macroscopic hard sphere interactions. All the other physical models we commonly used have nothing to do with the microscopic interactions. With beads and suitable beading methods,
one can make faithful molecular models of molecules.

Prof. Sonoda volunteered as TA in all of my workshops in Japan. He has now also become an expert of molecular beading. Here he tried to help Prof. Shinmyozu fix the beading problem.


Prof. Sonoda volunteered as TA in all of my workshops in Japan. He has now also become an expert of molecular beading. Here he tried to help Prof. Shinmyozu fix the beading problem.

Bead model of small stellated dodecahedron
Another class of bead models made by Mr. Horibe is the small stellated dodecahedron, which is one of the Kepler–Poinsot polyhedra.

The basic idea of making this kind of dendritic dodecahedra is to choose a suitable size of Goldberg polyhedron and then grow a short segment of endcapped carbon nanotube along each pentagon. In this particular case, the endcapped CNTs are just hemisphere of C20s. Similar trick to make dendrite-like structures is used in many of Mr. Horibe's work.

The basic idea of making this kind of dendritic dodecahedra is to choose a suitable size of Goldberg polyhedron and then grow a short segment of endcapped carbon nanotube along each pentagon. In this particular case, the endcapped CNTs are just hemisphere of C20s. Similar trick to make dendrite-like structures is used in many of Mr. Horibe's work.
Thursday, June 14, 2012
Mr. Horibe's story
Yesterday, Mr. Horibe informed me with email that he made the first regular polyhedron with duralumin tubes around 1975. After that he was busy on teaching and nothing was done for a while.
However, around 1995, he made the first bead model of dodecahedron which was consisting of 30 balls based on the problem described in the famous math book (Sangaku book, 算法助術) from the Edo period (江戶時代) of Japan. Since then, he started to make many different kinds of mathematical beadworks alone for about 17 years until we met last week. He said he will keep on making more bead models.
However, around 1995, he made the first bead model of dodecahedron which was consisting of 30 balls based on the problem described in the famous math book (Sangaku book, 算法助術) from the Edo period (江戶時代) of Japan. Since then, he started to make many different kinds of mathematical beadworks alone for about 17 years until we met last week. He said he will keep on making more bead models.
Wednesday, June 13, 2012
Two Sangaku books from Mr. Horibe
I also got two nice books on Sangaku (算額) from Mr. Horibe.
The first one is a reprint of a famous Japanese math book (算法助術) originally published in the early 19th century.

A page from this book:

The second one is the catalog for an exhibition on Sangaku in Nagoya a few years ago (2005).

A page from this beautiful catalog:

Mr. Horibe said, however, very few people came to this exhibition.
The first one is a reprint of a famous Japanese math book (算法助術) originally published in the early 19th century.

A page from this book:

The second one is the catalog for an exhibition on Sangaku in Nagoya a few years ago (2005).

A page from this beautiful catalog:

Mr. Horibe said, however, very few people came to this exhibition.
Sangaku and mathematical beading
Mr. Horibe, as a math teacher in Japan, is particularly interested in the connection between mathematical beading and the traditional Japanese temple mathematics, namely Sangaku (算額). His teacher and colleague, Hidetoshi Fukagawa ( 深川英俊), is famous for his work on Sangaku and published a book, Sacred Mathematics: Japanese Temple Geometry, with Princeton's physicist Tony Rothman.

There are a few questions of Sangaku which are related to tangent spheres. For instance, the following problem appears in Fujita Kagen’s 1796 edition of Shinpeki Sanpo. (Collection of Fukagawa Hidetoshi.)

The translation of this problem given in the "Sacred mathematics" is
"Twenty small balls of radius r cover one big ball of radius R where each small ball touches three other small balls. Find R in terms of r."
Another problem related to the bead model of C20 appeared in 1830 book Sanpo Kisho, or Enjoy Mathematics Tablets, by Baba Seitoku (1801–1860)
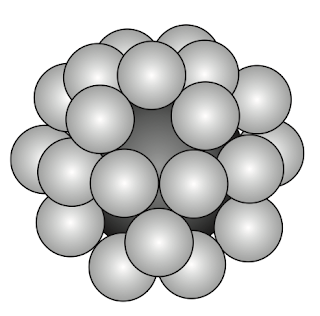
In this problem, small spheres correspond to beads that represent 30 edges of a dodecahedron.
To illustrate these two problems, Mr. Horibe made a beautiful, but non-standard bead model consisting of 20 ping-pong balls punctured with three holes at suitable places in order to connect them with an elastic rubber string. Of course, this model is a dodecahedron with ping-Pong balls located at the 20 vertices. Using the similar technique, he also made a bead model of an icosahedron consisting 12 Ping-Pong balls located at the vertices too.

To illustrate the second problem with 30 small spheres in touch with a large central sphere, Mr. Horibe did something even more amazing. He tried to make a composite bead model for the problem 2. This model consists of 30 small spheres outside (i.e. a dodecahedron) and a large sphere inside with small and large spheres satisfying the correct ratio of their radii, i.e. R=sqrt{5} r. This was a difficult task. Mr. Horibe quickly realized that it was very expensive to ask people to made two wooden beads exactly with this ratio. So he could only look around for different kind of balls in many stores in Japan, particularly he always brought a calculator and a ruler with him to measure if he was lucky enough to find out just the right beads that satisfied this condition. Quite fortunately, he found out a right size of metal ball for the central large sphere. So he made two nice models, one for Fukagawa and another for himself, for the famous Sangaku problem. In the following pictures I took at Nagoya's Children and Family Center, you can see how Mr. Horibe stretched the small spheres apart and pull the inner large sphere out. It was quite a show.


There are a few questions of Sangaku which are related to tangent spheres. For instance, the following problem appears in Fujita Kagen’s 1796 edition of Shinpeki Sanpo. (Collection of Fukagawa Hidetoshi.)

The translation of this problem given in the "Sacred mathematics" is
"Twenty small balls of radius r cover one big ball of radius R where each small ball touches three other small balls. Find R in terms of r."
Another problem related to the bead model of C20 appeared in 1830 book Sanpo Kisho, or Enjoy Mathematics Tablets, by Baba Seitoku (1801–1860)

In this problem, small spheres correspond to beads that represent 30 edges of a dodecahedron.
To illustrate these two problems, Mr. Horibe made a beautiful, but non-standard bead model consisting of 20 ping-pong balls punctured with three holes at suitable places in order to connect them with an elastic rubber string. Of course, this model is a dodecahedron with ping-Pong balls located at the 20 vertices. Using the similar technique, he also made a bead model of an icosahedron consisting 12 Ping-Pong balls located at the vertices too.

To illustrate the second problem with 30 small spheres in touch with a large central sphere, Mr. Horibe did something even more amazing. He tried to make a composite bead model for the problem 2. This model consists of 30 small spheres outside (i.e. a dodecahedron) and a large sphere inside with small and large spheres satisfying the correct ratio of their radii, i.e. R=sqrt{5} r. This was a difficult task. Mr. Horibe quickly realized that it was very expensive to ask people to made two wooden beads exactly with this ratio. So he could only look around for different kind of balls in many stores in Japan, particularly he always brought a calculator and a ruler with him to measure if he was lucky enough to find out just the right beads that satisfied this condition. Quite fortunately, he found out a right size of metal ball for the central large sphere. So he made two nice models, one for Fukagawa and another for himself, for the famous Sangaku problem. In the following pictures I took at Nagoya's Children and Family Center, you can see how Mr. Horibe stretched the small spheres apart and pull the inner large sphere out. It was quite a show.

Tuesday, June 12, 2012
Beadworks from the viewpoint of a chemist
The difference that Mr. Horibe and I see these bead models is probably due to our different backgrounds. Mr. Horibe is trained as a math teacher, while I am a theoretical chemist. Even though I am acquainted with some basic mathematics for my own researches, I emphasized the chemical implication of these bead models as a method to realize nanoscaled molecules and materials. For instance, I recognized how to correctly interpret these bead models microscopically immediately after I my first buckyball with beads was done. And I also fully appreciated the power of mathematical beading as a new, and powerful method to make arbitrary fullerenes and, later on, further extended the method to arbitrary molecules.
Collaborating with Chern, now a graduate student of chemistry in MIT, we quickly became familiar with topological and geometric aspects of certain graphitic structures. Of course, Chern Chuang plays a critical role. He is very good at geometry, especially polyhedra and minimal surfaces. He also likes to make all kind of mathematical models since he was a high school student. He worked out the necessary mathematics for describing many interesting graphic structures systematically for his Master degree thesis. At the beginning, his focus was on the carbon nanotori with a goal to find out their general structural rules. We believe we have a good understanding of them now. The main findings are summarized in two papers:
1. Chuang, C.; Fan, Y.-C.; Jin, B.-Y. Generalized Classification of Toroidal and Helical Carbon Nanotubes J. Chem. Info. Model. 2009, 49, 361-368.
2. Chuang, C; Fan, Y.-C.; Jin, B.-Y. Dual Space Approach to the Classification of Toroidal Carbon Nanotubes J. Chem. Info. Model. 2009, 49, 1679-1686.
We also submitted a paper entitled “Comments on Structural Types of Toroidal Carbon Nanotubes” to Chemistry European Journal last year. In this paper, we summarized the carbon nanotori in thirteen canonical achiral structures, which are related to each other through three types of geometric maniputations, namely rim rotation, horizontal shift, and generalized Stone-Wells transformations. Unfortunately, the paper was rejected because of the criticism we had on the paper by F. Beuerls et al.
We quickly realized that we could systematically create quite generally a large family of graphitic structures using carbon nanotori as building blocks. This includes helically coiled carbon nanotori (carbon helices for simplicity), carbon torus knots, high-genus fullerenes, singly-, doubly-, and triply periodic minimal surfaces. Of course, one can also have all kind of variations of pseudo-periodic minimal surfaces by using heptagons instead of octagons. Part of this endeavor is summarized in "Systematics of Toroidal, Helically-Coiled Carbon Nanotubes, High-Genus Fullerenes, and Other Exotic Graphitic Materials" (Procedia Engineering, 2011, 14, 2373-2385) by Chuang, C., Fan, Y.-C. and me. These graphitic structures can be succinctly summarized as follows:
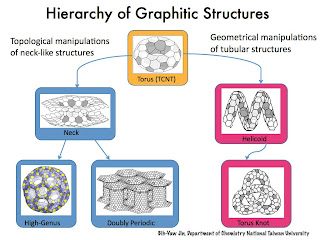
Collaborating with Chern, now a graduate student of chemistry in MIT, we quickly became familiar with topological and geometric aspects of certain graphitic structures. Of course, Chern Chuang plays a critical role. He is very good at geometry, especially polyhedra and minimal surfaces. He also likes to make all kind of mathematical models since he was a high school student. He worked out the necessary mathematics for describing many interesting graphic structures systematically for his Master degree thesis. At the beginning, his focus was on the carbon nanotori with a goal to find out their general structural rules. We believe we have a good understanding of them now. The main findings are summarized in two papers:
1. Chuang, C.; Fan, Y.-C.; Jin, B.-Y. Generalized Classification of Toroidal and Helical Carbon Nanotubes J. Chem. Info. Model. 2009, 49, 361-368.
2. Chuang, C; Fan, Y.-C.; Jin, B.-Y. Dual Space Approach to the Classification of Toroidal Carbon Nanotubes J. Chem. Info. Model. 2009, 49, 1679-1686.
We also submitted a paper entitled “Comments on Structural Types of Toroidal Carbon Nanotubes” to Chemistry European Journal last year. In this paper, we summarized the carbon nanotori in thirteen canonical achiral structures, which are related to each other through three types of geometric maniputations, namely rim rotation, horizontal shift, and generalized Stone-Wells transformations. Unfortunately, the paper was rejected because of the criticism we had on the paper by F. Beuerls et al.
We quickly realized that we could systematically create quite generally a large family of graphitic structures using carbon nanotori as building blocks. This includes helically coiled carbon nanotori (carbon helices for simplicity), carbon torus knots, high-genus fullerenes, singly-, doubly-, and triply periodic minimal surfaces. Of course, one can also have all kind of variations of pseudo-periodic minimal surfaces by using heptagons instead of octagons. Part of this endeavor is summarized in "Systematics of Toroidal, Helically-Coiled Carbon Nanotubes, High-Genus Fullerenes, and Other Exotic Graphitic Materials" (Procedia Engineering, 2011, 14, 2373-2385) by Chuang, C., Fan, Y.-C. and me. These graphitic structures can be succinctly summarized as follows:

TCNTs with no latitude coordinates
In addition to the eight structural types of carbon nanotori, Chern also showed that there are five other different tori without latitude coordinates defined. Chern also gave the systematic transformation rule, which we call the generalized Stone-Wells transformation, to derive them from classes A, B, and E, respectively.
Of course, Mr. Horibe has made many different structural types of tori with beads as shown in the following photo taken in the Nagoya's Children and Family Center. One can see he enjoyed making tori with 7- up to 9-fold rotational symmetry quite a lot. However, I didn't check very carefully how many different types of tori (according to our classification scheme) he has done.

I also discovered that he has a few tori without latitude coordinates. Incidentally, I found that Mr. Horibe had made a particular torus which is exactly the same as the one (class K) that appeared in one of slides of my introductory talk given in the Nagoya's Children and Family Center. Even the color codings are the same. Quite amazing.

Of course, Mr. Horibe has made many different structural types of tori with beads as shown in the following photo taken in the Nagoya's Children and Family Center. One can see he enjoyed making tori with 7- up to 9-fold rotational symmetry quite a lot. However, I didn't check very carefully how many different types of tori (according to our classification scheme) he has done.

I also discovered that he has a few tori without latitude coordinates. Incidentally, I found that Mr. Horibe had made a particular torus which is exactly the same as the one (class K) that appeared in one of slides of my introductory talk given in the Nagoya's Children and Family Center. Even the color codings are the same. Quite amazing.

Two gifts from Mr. Horibe
I am usually the person who gave people beadworks as gifts. But I myself got a beaded C60 as a gift from Mr. Horibe on our visit to his home. And the next day, when he participated my workshop in Nagoya, I got another giant torus as a gift.


His model is quite different from mine because most often he used only a single elastic rubber band with exact length to make his beadworks. In this sense, the path of his elastic string exactly corresponds to the Hamiltonian path exactly and has, of course, the minimal length for a particular model. So, the elastic string passed every bead in the model twice and only twice. To avoid beads fall apart, Mr. Horibe then made a knot in the end. So you can pull or press his bead models to some extent.
Possibly due to his training as mathematics teacher, he always uses a single string even for structures that contain more several thousand beads. I was quite surprised when I just heard of it. Just imagine how one can use a single string to bead the giant green stellated dodecahedron as shown in the following photo. The problem is that it would become very difficult to bead with such a long string. The good thing is that the path of string in his case is really a Hamiltonian path no matter how many beads a model contains. I guess that he also needed to plan well before he started because it is not always trivial to find out the Hamiltonian path. Sometimes, we just got trapped as weaving process goes. I don't know how he managed to do it with only one string especially for certain structures that has more than several thousand beads.

Another practical aspect about using elastic string is that elastic string is much thicker than the Nylon string I typically used. I suspect that it may not easy to pass it through three times through a hole. But of course, it is not a good idea to pass string through some beads twice, but some other beads three times because that will make the tension generated by the rubber band uneven throughout the structure. There is no such problem for the Nylon string because the bead models made by Nylon string are usually quite strong and hard. So it is harder to deform them like the model made with elastic rubber band.


His model is quite different from mine because most often he used only a single elastic rubber band with exact length to make his beadworks. In this sense, the path of his elastic string exactly corresponds to the Hamiltonian path exactly and has, of course, the minimal length for a particular model. So, the elastic string passed every bead in the model twice and only twice. To avoid beads fall apart, Mr. Horibe then made a knot in the end. So you can pull or press his bead models to some extent.
Possibly due to his training as mathematics teacher, he always uses a single string even for structures that contain more several thousand beads. I was quite surprised when I just heard of it. Just imagine how one can use a single string to bead the giant green stellated dodecahedron as shown in the following photo. The problem is that it would become very difficult to bead with such a long string. The good thing is that the path of string in his case is really a Hamiltonian path no matter how many beads a model contains. I guess that he also needed to plan well before he started because it is not always trivial to find out the Hamiltonian path. Sometimes, we just got trapped as weaving process goes. I don't know how he managed to do it with only one string especially for certain structures that has more than several thousand beads.

Another practical aspect about using elastic string is that elastic string is much thicker than the Nylon string I typically used. I suspect that it may not easy to pass it through three times through a hole. But of course, it is not a good idea to pass string through some beads twice, but some other beads three times because that will make the tension generated by the rubber band uneven throughout the structure. There is no such problem for the Nylon string because the bead models made by Nylon string are usually quite strong and hard. So it is harder to deform them like the model made with elastic rubber band.
Monday, June 11, 2012
Bead models of dodecahedron and icosahedron
Mr. Horibe started to play with polyhedral models very early. According to him, he has constructed Platonic models with a long cylindrical tube capped with two beads when he was still an undergraduate student in the 70s.
He demonstrated in front of us that dodecahedron and icosahedron are dual to each other using this kind of models. With long cylindrical tubes, the whole structure becomes very flexible, so you can compress it and put one inside the other. Students can realize, through this amazing way, why dodecahedron and icosahedron are dual to each other. I can only say that Mr. Horibe must be a very effective math teacher. I wish I could learn math from him when I was a high school student.



In some sense, this kind of bead models is very similar to the so-called tensegrity structures. BTW, Mr. Horibe usually uses a single elastic string for making his bead models, which makes his models even more flexible and bendable. I will comment more on this aspect later.
He demonstrated in front of us that dodecahedron and icosahedron are dual to each other using this kind of models. With long cylindrical tubes, the whole structure becomes very flexible, so you can compress it and put one inside the other. Students can realize, through this amazing way, why dodecahedron and icosahedron are dual to each other. I can only say that Mr. Horibe must be a very effective math teacher. I wish I could learn math from him when I was a high school student.



In some sense, this kind of bead models is very similar to the so-called tensegrity structures. BTW, Mr. Horibe usually uses a single elastic string for making his bead models, which makes his models even more flexible and bendable. I will comment more on this aspect later.
Some more amazing beadworks of Horibe with comments on colors in bead models
Most of Horibe’s beadworks are made by single color. Unlike beadworks made by my group, I usually decorated nonhexagons with different colors or use colors to represent single and double bonds. Of course, this will spoil the color of hexagons and nonhexagons. It is not possible to use colors independently for hexagons and nonhexagons. There must be some polygons, which will be decorated with more than two colors when one chooses to use more than one color. According to him, that is the reason he usually used single color to do beading to avoid this situation. Only in a few examples he used two colors to illustrate some particular features.


But, to chemists, using colored beads seems to be an obvious choice. Chemists have been using many kinds of molecular models to represent microscopic structures of molecules. It is quite common to use different colors to denote different kind of atoms. Now, in bead models, we move the emphasis from atoms to bonds. It is still apparent that one could also employ colors to mean different things. Faces in a molecular network do not have important chemical meanings as those of vertices (atoms) and edges (chemical bond). But more importantly, we would view the color pattern as a new dimension of beaded molecules, which can not only give geometric or chemical meaning, but also make them more visually pleasing.


But, to chemists, using colored beads seems to be an obvious choice. Chemists have been using many kinds of molecular models to represent microscopic structures of molecules. It is quite common to use different colors to denote different kind of atoms. Now, in bead models, we move the emphasis from atoms to bonds. It is still apparent that one could also employ colors to mean different things. Faces in a molecular network do not have important chemical meanings as those of vertices (atoms) and edges (chemical bond). But more importantly, we would view the color pattern as a new dimension of beaded molecules, which can not only give geometric or chemical meaning, but also make them more visually pleasing.
Visiting Horibe and workshop at Nagoya Child and Family Center
Under the great arrangement of prof. Sonoda, I have this opportunity to visit Mr. Horibe in his place in the Aichi prefecture last Saturday (6/9/2012), two days before I returned back to Taiwan. It was really nice to meet him and saw many of his amazing mathematical beadworks. But, he doesn't speak English, so I can only communicate with him mainly through the translation of Prof. Sonoda. Most often, they spoke to each other in Japanese. But I still had plenty of time taking pictures and inspected his beadworks. I hope my understanding about his work is correct. I will post some of his beadworks and also compare his works with mine in the next few posts. But what I wrote could be my misunderstanding.


I knew Mr. Horibe and his beadworks through Prof. Sonoda two years ago. As I mentioned before that Prof. Sonoda is a missionary of cube kaleidoscope and has the passion to share this activity to kids all over the world. He visited Taiwan two years ago to give not only his own chemistry research, but also a workshop on the cube kaleidoscope. I participated both events and also shown him my works on beaded molecules. After he returned to Japan, he knew quite accidentally from a secretary of Prof Ono that a local high school teacher had set up a website which contains a lot of similar mathematical beadworks. So prof. Sonoda informed me about Horibe's beadworks immediately. Finally we have the chance to meet each other.
On Sunday, Mr. Horibe and his wife also participated the workshop held at Nagoya Child and Family Center near B's Hotel hosted by Ms Hiroe Takeuchi (6/10/2012).


I knew Mr. Horibe and his beadworks through Prof. Sonoda two years ago. As I mentioned before that Prof. Sonoda is a missionary of cube kaleidoscope and has the passion to share this activity to kids all over the world. He visited Taiwan two years ago to give not only his own chemistry research, but also a workshop on the cube kaleidoscope. I participated both events and also shown him my works on beaded molecules. After he returned to Japan, he knew quite accidentally from a secretary of Prof Ono that a local high school teacher had set up a website which contains a lot of similar mathematical beadworks. So prof. Sonoda informed me about Horibe's beadworks immediately. Finally we have the chance to meet each other.
On Sunday, Mr. Horibe and his wife also participated the workshop held at Nagoya Child and Family Center near B's Hotel hosted by Ms Hiroe Takeuchi (6/10/2012).

Sunday, June 10, 2012
Friday, June 8, 2012
Construction procedure of C60 (Japanese translation)
Prof. Sonoda made a nice Japanese translation of the detailed construction described in the supporting information of the article, Molecular Modeling of Fullerenes with Beads, J. Chem. Edu 2012 , 89 (3), 414–416.", by Prof. Cuccia and me.



Also, here is the original English version of the first page, the next two pages are the same.




Also, here is the original English version of the first page, the next two pages are the same.

Japanese translation of 珠璣科學─串珠碳六十
Prof. Inoue (井上吉教) of Hikone prefecture university and one of his Chinese students kindly translated my article "珠璣科學─串珠碳六十" (The Science of Beading - Beaded C60) with Dr. Tsoo for the March issue of the "Science Monthly (科學月刊)" magazine.

(New post, scanned images 6/12/2012)




Prof. Inoue also made a few fullerenes as shown in the following pictures. I didn`t check them very carefully. Possibly, one of them is the icosahedral C80 and another is the cylindrical shape C84. There seems to be a fullerene belonging to D3h point group.



(New post, scanned images 6/12/2012)





Prof. Inoue also made a few fullerenes as shown in the following pictures. I didn`t check them very carefully. Possibly, one of them is the icosahedral C80 and another is the cylindrical shape C84. There seems to be a fullerene belonging to D3h point group.


Monday, June 4, 2012
Workshop at the Ito campus of Kyushu University
Sunday, June 3, 2012
Workshop at the Fukuoka Gender Equality Promotion Center
Workshop with children and family members of NPO Community of the Culture with and for
Children and some members of UPA Owl Association as well as Prof. Masahito Katayama at AMIKAS(Fukuoka Gender Equality Promotion Center) hosted by Takaaki Sonoda and Yumiko Takamiya and assisted by Yasushi Kita and Kumiko Okayama.
Talk with the title: "Chemistry, geometry, and art: constructing fullerenes with beads". The materials and bead models I brought to Japan:
Talk with the title: "Chemistry, geometry, and art: constructing fullerenes with beads". The materials and bead models I brought to Japan:
Subscribe to:
Posts (Atom)









