Compared with other methods for building physical models of fullerenes, the beaded molecules have many advantages:
1. The hard-sphere interactions among beads correctly mimic the microscopic valence-shell repulsion.
2. The only information needed to build a particular fullerene with a spiral is completely encoded in its spiral code.
3. The resulting shape of a beaded fullerene is in good agreement with the real geometry of the corresponding fullerene.
4. The mechanical response of a beaded molecule is related to that of a true fullerene molecule under pressure.
5. The beaded molecule can be made quite compact by using beads with small diameters. The sizes of the beaded molecules for fullerenes with even several hundreds of carbon atoms are less than 10 cm, which can be held in hand easily; while using the commercial models for the same fullerene, the sizes are typically much larger.
6. The resulting beaded molecules are aesthetically pleasing.
7. The structures of beaded molecules are stable, robust, and durable.
Monday, April 30, 2007
Thursday, April 26, 2007
Wednesday, April 25, 2007
The Beaded Models of 12 Stable T240 isomers
Finally, I have all 12 isomers of T240:

The corresponding computer-generated geometry for these models are

The one with orange color is the newest T240 I made. I knew this one should exist long time ago. But I don't know why I didn't make this one until a few weeks ago.
The first three tori in the bottom row are chiral isomers of T240. I have only made one for each pair of the enantiomers. If these three are counted twice, the total number of stable isomers of T240 should be 15 as I mentioned before.
Among all of these models, I like the four in the first row and the three in the right column most because the symmetry and shape these six isomers have. In fact I have made several duplicates of the top four and the middle one in the right column. But all of them have been given away as souvenir. Now these are the only T240 I have.

The corresponding computer-generated geometry for these models are

The one with orange color is the newest T240 I made. I knew this one should exist long time ago. But I don't know why I didn't make this one until a few weeks ago.
The first three tori in the bottom row are chiral isomers of T240. I have only made one for each pair of the enantiomers. If these three are counted twice, the total number of stable isomers of T240 should be 15 as I mentioned before.
Among all of these models, I like the four in the first row and the three in the right column most because the symmetry and shape these six isomers have. In fact I have made several duplicates of the top four and the middle one in the right column. But all of them have been given away as souvenir. Now these are the only T240 I have.
Another large Truncated Tetrahedron
Chuang Chern made another large truncated tetrahedron as shown below.

This one has the horizontal armchair pattern if we define the horizontal direction as shown on the left of the figure , in contrast with the previous large truncated tetrahedron that has zigzag pattern horizontally.
Incidentally, we also have armchair pattern along any direction that connects two pentagons in the current model.

This one has the horizontal armchair pattern if we define the horizontal direction as shown on the left of the figure , in contrast with the previous large truncated tetrahedron that has zigzag pattern horizontally.
Incidentally, we also have armchair pattern along any direction that connects two pentagons in the current model.
Tuesday, April 24, 2007
Another large Torus and the orgin of pentagon patterns
Here is another large chiral Torus I made a few months ago. It is easy to see the two pattern of pentagons: a smaller one formed by grey beads and a large one formed by the beads with orange color.

I have designed this torus such that the pentagonal patterns formed by the beads can be vividly shown with different colors I chose. These pentagonal patterns are hidden when the typical ball-and-stick models are used to represent the corresponding fullerenes. It appears only in the bead-representation of the fullerenes. The reason is that the beads, located at the center of bonds, form a straight line in the beaded model even though the bonds in the ball-and-stick model exhibit zig-zag pattern.
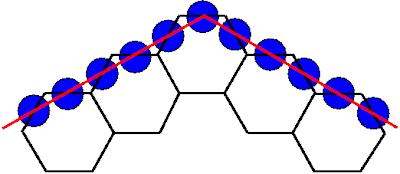

I have designed this torus such that the pentagonal patterns formed by the beads can be vividly shown with different colors I chose. These pentagonal patterns are hidden when the typical ball-and-stick models are used to represent the corresponding fullerenes. It appears only in the bead-representation of the fullerenes. The reason is that the beads, located at the center of bonds, form a straight line in the beaded model even though the bonds in the ball-and-stick model exhibit zig-zag pattern.

Fluorescent T120 keychain
I made this T120 keychain with fluorescent beads. Compared with C60 keychain, I believe that T120 is even more suitable for this purpose. This is because T120 is flat, while C60 is round. When you put a C60 keychain in your pocket for a few days, the line that holds the ball tight can easily become loose and relaxed. The T120 keychain does not seem to have this problem.


Friday, April 20, 2007
Large Truncated Tetrahedral and Octahedral Fullerenes
Chuang Chern made this amazing truncated tetrahedron which consists of more than a thousand beads. I guess he probably spent more than 10 hours on this gigantic fullerene. This structure is essentially a natural extension of the system with T or Td symmetry as I shown before. All fullerenes belonging this catagory can be completely specified by two vectors, a and b. The first vector, a, denotes the relative arrangement among the three pentagons at each vertex as shown in the right figure below. When these three pentagons are not nearest neighbours with each other, the resulting tetrahedron becomes a truncated one, just like the one I have posted below.
The second vector, b, specifies the separation between two pentagons, belonging to two neighbouring vertices separately.

Now let's imagine we have a continuous Achimedean solid just like our truncated beaded tetrahedron which can be described by the same two vectors, a and b. Now let the vector b gradually changes to zero, then this tetrahedron will be continuously transformed into an octahedron. The following figure taken from Wikipedia demonstrates this can be done graphically.
However, this is not possible in fullerene cages due to the intrinsic physical properties of the graphitic sheet. The smallest possible value of b is when these two pentagons are separated by one hexagon. We can't fuse two pentagons into one, the Euler theorem will be violated then. Additionally, since there are six vertices in an octahedron, every vertex of an octahedron must contain two pentagons. So the four faces around any one of the six vertices cannot be all the same. The two triangular faces lies along the direction defined by these two pentagons, the direction of vector b, will be different from the other two faces lying perpendicular to this direction. But when another vector, a, is very large, the truncated tetrahedron will approach the octahedron if the detailed structure around the vertices is ignored!
In general, it is not possible to have a fullerene with the octahedron symmetry, if only 5- and 6-member rings are allowed.
The second vector, b, specifies the separation between two pentagons, belonging to two neighbouring vertices separately.

Approaching the Octahedral Limit
Now let's imagine we have a continuous Achimedean solid just like our truncated beaded tetrahedron which can be described by the same two vectors, a and b. Now let the vector b gradually changes to zero, then this tetrahedron will be continuously transformed into an octahedron. The following figure taken from Wikipedia demonstrates this can be done graphically.

However, this is not possible in fullerene cages due to the intrinsic physical properties of the graphitic sheet. The smallest possible value of b is when these two pentagons are separated by one hexagon. We can't fuse two pentagons into one, the Euler theorem will be violated then. Additionally, since there are six vertices in an octahedron, every vertex of an octahedron must contain two pentagons. So the four faces around any one of the six vertices cannot be all the same. The two triangular faces lies along the direction defined by these two pentagons, the direction of vector b, will be different from the other two faces lying perpendicular to this direction. But when another vector, a, is very large, the truncated tetrahedron will approach the octahedron if the detailed structure around the vertices is ignored!
In general, it is not possible to have a fullerene with the octahedron symmetry, if only 5- and 6-member rings are allowed.
Wednesday, April 18, 2007
Another chiral twisted T240 with small inner-rim
Sunday, April 15, 2007
Torus Keychain
My daughter and wife help me make this keychain.

Although I have seen many buckyball keychains in the craft store, "Little Bear's Mom", near the Taipie's main train station (延平北路的小熊媽媽). But I believe the one I made is probably the first nanotorus keychain. The shape of torus is even more suitable for the purpose of the keychain.

Although I have seen many buckyball keychains in the craft store, "Little Bear's Mom", near the Taipie's main train station (延平北路的小熊媽媽). But I believe the one I made is probably the first nanotorus keychain. The shape of torus is even more suitable for the purpose of the keychain.
Saturday, April 14, 2007
Strongly distorted tori again
In the last post, I mentioned that I didn't make beaded models for the isomers, I5 and II5. Both of these two chiral isomers belong to twisted form from the parent compounds, I1 and II1. In fact, I have examined this kind of chiral torus on a post about "Strongly Distorted Tori" in Nov. 2006.
http://thebeadedmolecules.blogspot.com/2006/12/strongly-distorted-tori.html
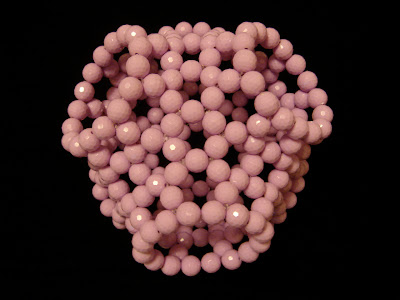
Based on these experiences, I originally thought that I5 and II5 are both unstable. Now Chuang's simple force field suggests that they are stable. Maybe this is because the inner-rim of I5 is small. I made a beaded model for I5 tonight as shown in the following picture.

We can see from this picture, the distorion in the inner-rim is quite significant, which is different from the computer-optimized geometry. Apparently, this is due to the mismatch of beads in the outer-rim. Although the distortion of I5 can be considered as small if we compare its geometry with the physical models I made a few months ago, I still tend to elimininate these twisted isomers from the list of stable isomers. Hence, there should be only 15 important isomers, instead of 19 isomers for the T240. Or only 12 isomers if we only count two mirror images of a pair of chiral compouds as one compound.
Surprisingly, this number is exactly the same as the prediction I made last December,
http://thebeadedmolecules.blogspot.com/2006/12/ten-isomers-of-t240.html,
where I suggested that there should be 12 isomers, although I only made 10 of them. Of course, there are some differences. It is obvious now there are only two isomers for D5h symmetry. But, I thought there should be 3 isomers at that time. The completely new isomer of T240 is the only one belonging to the type IV system: molecular innertube, which, I guess, couldn't find without Chuang's newly developed generalized classification scheme of toroidal carbon nanotubes.
http://thebeadedmolecules.blogspot.com/2006/12/strongly-distorted-tori.html
Based on these experiences, I originally thought that I5 and II5 are both unstable. Now Chuang's simple force field suggests that they are stable. Maybe this is because the inner-rim of I5 is small. I made a beaded model for I5 tonight as shown in the following picture.

We can see from this picture, the distorion in the inner-rim is quite significant, which is different from the computer-optimized geometry. Apparently, this is due to the mismatch of beads in the outer-rim. Although the distortion of I5 can be considered as small if we compare its geometry with the physical models I made a few months ago, I still tend to elimininate these twisted isomers from the list of stable isomers. Hence, there should be only 15 important isomers, instead of 19 isomers for the T240. Or only 12 isomers if we only count two mirror images of a pair of chiral compouds as one compound.
Surprisingly, this number is exactly the same as the prediction I made last December,
http://thebeadedmolecules.blogspot.com/2006/12/ten-isomers-of-t240.html,
where I suggested that there should be 12 isomers, although I only made 10 of them. Of course, there are some differences. It is obvious now there are only two isomers for D5h symmetry. But, I thought there should be 3 isomers at that time. The completely new isomer of T240 is the only one belonging to the type IV system: molecular innertube, which, I guess, couldn't find without Chuang's newly developed generalized classification scheme of toroidal carbon nanotubes.
Friday, April 13, 2007
19 Isomers of T240
Here is the list of stable isomers of T240. According to Chuang's generation algorithm for the toroidal compounds, there are 40 isomers for T240. By simple inspection, I think more than half of them are probably unstable, particularly those with very large radius and very small girth. If chiral compounds are not counted twice, there are 14 isomers. These stable isomers can be classified into five type based on the arrangement of heptagons in the inner-rim as shown in the following figures.
Currently, I have created the beaded models for 12 of them. Only I5 and II5 are missing. This kind of isomers is related to their parent isomers, I1 and II1 by twisting the upper and lower parts of the torus respectively.
According to my previous experience, the isomers generated by this kind of transformation seem to be quite unstable as shown in one of my previous post. But the calculation based on Chuang's simple force field suggests that this kind of isomers could sometimes be stable depending on the type of inner-rim.
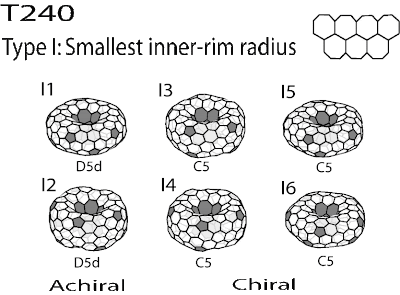
No beaded models for I5 and I6.
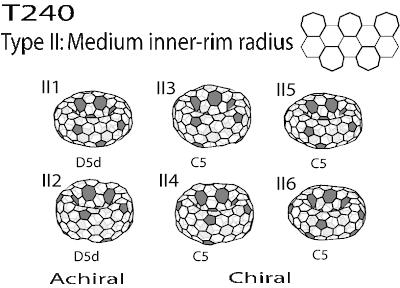
No beaded models for II5 and II6.
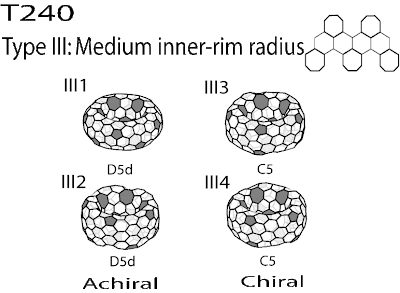


The tori in these figures are generated by the matlab scripts written by Chuang Chern, possibly with many useful discussions with Fan Yuan-Jia.
Currently, I have created the beaded models for 12 of them. Only I5 and II5 are missing. This kind of isomers is related to their parent isomers, I1 and II1 by twisting the upper and lower parts of the torus respectively.
According to my previous experience, the isomers generated by this kind of transformation seem to be quite unstable as shown in one of my previous post. But the calculation based on Chuang's simple force field suggests that this kind of isomers could sometimes be stable depending on the type of inner-rim.

No beaded models for I5 and I6.

No beaded models for II5 and II6.



The tori in these figures are generated by the matlab scripts written by Chuang Chern, possibly with many useful discussions with Fan Yuan-Jia.
Bottle with a large wide mouth
I found a bottle with a large and wide mouth I bought more than ten years ago from the Disney land, which is perfect for the storage of my beaded models.


| From New Album 2007/4/8 PM 12:53 |


Thursday, April 12, 2007
The little beaded bag of my niece
Wednesday, April 11, 2007
Large-hole Torus 120
I have posted two isomers of T120 last November.
http://thebeadedmolecules.blogspot.com/2006/11/carbon-240.html
Both of these two isomers have the same type of inner-rim. The arrangements of the pentagons in the outer-rim for these two isomers are related to each other through Stone-Wales transformation.
Here is the beaded model with 10mm faceted beads for another isomer of T120. This one has larger hole due to the relative position among the heptagons in the inner-rim. The perimeter around the girth is also smaller than those of previous two isomers.

http://thebeadedmolecules.blogspot.com/2006/11/carbon-240.html
Both of these two isomers have the same type of inner-rim. The arrangements of the pentagons in the outer-rim for these two isomers are related to each other through Stone-Wales transformation.
Here is the beaded model with 10mm faceted beads for another isomer of T120. This one has larger hole due to the relative position among the heptagons in the inner-rim. The perimeter around the girth is also smaller than those of previous two isomers.

Tuesday, April 10, 2007
Giant Torus? A Joke?
It's real. How many beads are used in this model? What is this model corresponding to? How long does Chuang spend in making this model?

It is not hard to imagine that in a multilayer graphitic system, it is likely to have many holes connecting different sheets in the system. This picture in fact stands for the simplest situation.
Another possibility is the carbon Riemann sheets. Chuang has written a matlab program to generate this type of carbon systems. If I find the code, I will post it later. Maybe he can do it himself. Unfortunately, we don't have the beaded model for this kind of material yet. I probably have to find an undergrad to help me.

It is not hard to imagine that in a multilayer graphitic system, it is likely to have many holes connecting different sheets in the system. This picture in fact stands for the simplest situation.
Another possibility is the carbon Riemann sheets. Chuang has written a matlab program to generate this type of carbon systems. If I find the code, I will post it later. Maybe he can do it himself. Unfortunately, we don't have the beaded model for this kind of material yet. I probably have to find an undergrad to help me.
Carbon torus with 6-fold rotational axis
Monday, April 9, 2007
D-Type Schwartzite
Well, here is the D-Type Schwartzite with all heptagons in blue. It is easy to see that there is a three-fold rotational symmetry axis along each pod. Totally, there are 3x4=12 heptagons in a unit cell.
This structure is similar to the molecular tetrapod I posted before. However, there are some restrictions due to the patching condition between the tube and endcaps for the same reason as the situation in the endcapped nanotubes. For instance, the tetrapod I made has larger girths.


This structure is similar to the molecular tetrapod I posted before. However, there are some restrictions due to the patching condition between the tube and endcaps for the same reason as the situation in the endcapped nanotubes. For instance, the tetrapod I made has larger girths.

A New Model of P-Type Schwartzite
Sunday, April 8, 2007
Schwartzite and Torus
The structure of P-Type Schwartzite may look pretty complicated at first sight. It is not easy to see the construction rule. Chuang Chern noticed that there is an interesting connection between Schwartzite and Torus. Since Schwartzite structure has no positive Gaussian curvature, but the torus has both positive and negative curbatures. In the outer-rim, a torus has five or sixe pentagons to generate the effect of positive curvature, while in the inner-rim there are the same number of heptagons.
It is not too surprising to find that the connection necks from one hole to another hole in a Schwartzite are actually the inner-rims of the torus. By symmetry, one unit cell of P-type Schwartzite can be considered as assembly of six the inner-rim of 4-fold tori. Each neck contain 4 (or 8) heptagons, which can simulate the negative Gaussiuan curvatures. So in one unit cell there are 24 heptagons.

(Picture added 4/20/2007)
Similarly, there are 3 (or 6) heptagons in each neck of the D-type Schwartzite.
However, there are some difference too. Due to the strong strain energy in the outer-rim , it is not easy to have 3- or 4-fold torus.
It is not too surprising to find that the connection necks from one hole to another hole in a Schwartzite are actually the inner-rims of the torus. By symmetry, one unit cell of P-type Schwartzite can be considered as assembly of six the inner-rim of 4-fold tori. Each neck contain 4 (or 8) heptagons, which can simulate the negative Gaussiuan curvatures. So in one unit cell there are 24 heptagons.

(Picture added 4/20/2007)
Similarly, there are 3 (or 6) heptagons in each neck of the D-type Schwartzite.
However, there are some difference too. Due to the strong strain energy in the outer-rim , it is not easy to have 3- or 4-fold torus.
P-type Carbon Schwartzite: Periodic Minimal Surface
Chuang Chern made this beautiful model of carbon Schwarzite of type P a few months ago. I didn't take picture for this model until now. There are some other types of Schwartzites such as the type D system, which I have made one right after I saw Chuang's work.
Although the details of weaving are quite complicated, the resulting beaded model is beautiful. It is easy to see that the P-type Schwartzite as shown in the figure (just one unit cell) belongs the octahedral symmetry. Due to the translational symmetry, the whole periodical structure can be extended along six directions indefinitely. I wish we can make a beaded model with eight-unit cell for this system.

This model is made of 10mm faceted beads. The physical dimension is much larger compared with the other models (4mm beads usually) we have made.
In one of pictures in the previous post, if you are careful enough, you should be able to find a beaded model corresponding to the D-type Schwartzite.
Although the details of weaving are quite complicated, the resulting beaded model is beautiful. It is easy to see that the P-type Schwartzite as shown in the figure (just one unit cell) belongs the octahedral symmetry. Due to the translational symmetry, the whole periodical structure can be extended along six directions indefinitely. I wish we can make a beaded model with eight-unit cell for this system.

This model is made of 10mm faceted beads. The physical dimension is much larger compared with the other models (4mm beads usually) we have made.

In one of pictures in the previous post, if you are careful enough, you should be able to find a beaded model corresponding to the D-type Schwartzite.
Carbon Innertube
According to Chuang's exhausted search of carbon tori with 240 atoms and simultaneously satisfying C5 rotational symmetry and IPR (Independent Pentagon Rule), there are many possible isomers for T240. Out of these compounds, I found 19 stable isomers which I discussed in our group blog before (http://byjingroup.blogspot.com/). Here is one of T240 with a shape very similar to innertube.

Moreover, I suspect this is the only fullerene with this shape. I don't have proof, though.
Optimized shape of this molecule generated by Chuang.


Moreover, I suspect this is the only fullerene with this shape. I don't have proof, though.
Optimized shape of this molecule generated by Chuang.

One more carbon Archimedean
Molecular Tetrahedrons
I made several tetrahedral shape of fullerenes. These three tetrahedron belongs to Td, T, Td point group, respectively. I generate these fullerenes using the rule similar to that I used for higher fullerenes. But I believe that It is worthy to work out the systematic rule to generate these tetrahedron.
This molecule is a chiral fullerene.
[Strange? This post disappear automatically.]
Friday, April 6, 2007
Endcapped nanotubes
I just finished writing the section on the influence of endcaps on the nanotube's shape in my "The beaded molecules I. Spheroids" paper. I put my emphasis on (5,5) and (9,0) SWNT with the C60 endcaps, which is fine. I thought there should be a more systematic study on the effect of endcaps from the beaded molecule's viewpoints. This should include the patching conditions, chiral nanotubes and the effect on the shape change. I have no doubt that many of the issues I raised here probably have been treated before. I still think it is worthy to do it with the beaded molecules.






Wednesday, April 4, 2007
The effect of endcaps on the shapes of nanotubes
Supprising results do occur every time I try to make a new type of beaded molecules. For instance, I didn't expect to find anything particular interesting about the endcaps of the nanotube. I have built two short nanotubes endcapped with C60 along the five-fold symmetry axis more than two months ago. I have also taken a few pictures for these molecules. Well, the result looks good, the tubes are just like perfect cylinders. This is probably because there is little difference between five-fold symmetry and perfect rotational symmetry around the central axis. The lower symmetry of endcaps does not seems to produce broken symmetry. Or may be the effect is too small to notice at first sight.
I made another tube also with C60 endcaps, but instead of along five-fold symmetry axis, this time I patch the tube with the three-fold symmetry axis. I was amazed by the broken symmtry of the nanotube induced by the three-fold endcaps. Since there are many possible ways to connect the tube with the endcaps, depending on the relative orientation of the two endcaps. I found that the resulting endcapped nanotube can be either achiral or chiral, even though the uncapped nanotube is achiral. I wonder whether other people have noticed these interesting situations or not?
I made another tube also with C60 endcaps, but instead of along five-fold symmetry axis, this time I patch the tube with the three-fold symmetry axis. I was amazed by the broken symmtry of the nanotube induced by the three-fold endcaps. Since there are many possible ways to connect the tube with the endcaps, depending on the relative orientation of the two endcaps. I found that the resulting endcapped nanotube can be either achiral or chiral, even though the uncapped nanotube is achiral. I wonder whether other people have noticed these interesting situations or not?
Tuesday, April 3, 2007
Higher Fullerenes with I or Ih symmetry
Construction of higher fullerenes belonging either to I or Ih point groups is an interesting experience to me. There are not many of them, compared with all possible isomers. It seems to me it is not necessary to use the spiral algorithm I describe before. The symmetry of the systems pose a strong limitation on the possible positions of pentagons. By inspection, we can find out the systematic strategy for generating all possible higher fullerenes. I will explain my strategy later. Here are all possible I or Ih fullerene with the number of carbon atoms less 300.
C60(Ih), C80(Ih), C140(I), C180(Ih), C240(Ih), C260(I)

Chiral Compounds:

Honestly speaking, the colors I chose for these compounds are terrible. I am thinking about remaking these models. Maybe some of you can help.
C60(Ih), C80(Ih), C140(I), C180(Ih), C240(Ih), C260(I)

Chiral Compounds:

Honestly speaking, the colors I chose for these compounds are terrible. I am thinking about remaking these models. Maybe some of you can help.
Beaded Archimedean
In last two months, I was quite busy, and couldn't find time to create new beaded molecules. Part of reason is that I thought I have basically understood the most important things about beaded molecules, the only thing left is to write down the details. But now I know that the potential of physical modelling with beading is much broader. It is worthy to spend more time to explore the other applications of beading.
Here is a new beaded molecule I find interesting:

Here is a new beaded molecule I find interesting:

Subscribe to:
Posts (Atom)












