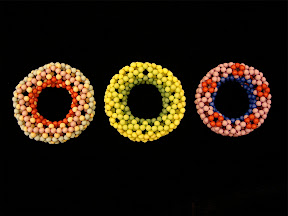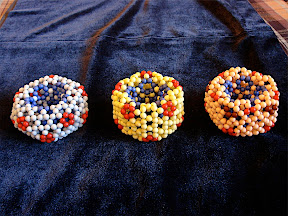A few weeks ago, when shopping with my wife in one of local stores which supplies all kinds of craft stuffs in Taipei, I was soon attracted by those beaded 3-D beadworks in the store. Standing in front of these cute artworks, I started to ponder about the possibility to use these beads to model the structure of molecules. But what kind of molecules? Due to the richness of chemical bonds, I know I could not use beads for every possible bond types. With only a little thought, I realized that beads are perfect for constructing molecular models of carbon fullerene, C
60, higher fullerenes, and nanotubes. More importantly, it seems that even much more complicated structures with shapes like spheroids and toroids can be made from the beads. To check my preliminary thought, I decided to buy some necessary materials to start with. These include three packs of 10mm beads and a roll of fishing line.
As my first molecular beading project, I chose the simplest fullerene, C
60, which is a truncated icosahedron consisted of 60 carbon atoms. At the beginning, I don't know anything about the weaving technique. Fortunately, my wife has some experiences. So under her guidance, I learned the basic technique, later I know that this technique is the so-called right-angle weaving. Here is the first beaded C60 I constructed:
(Beaded ball with 10mm beads.)
After I finished my first beaded molecule, I soon realized that the molecule I made is not really the so-called buckyball, C
60 with beads corresponding to the atoms. In fact, the beaded ball I made is composed of 90 beads, instead of 60 beads! What went wrong? If we examine carefully the structure of the beaded ball, we can see that there are four beads surrounding each bead! This is not allowed in the trivalent carbon compounds as we know. Each carbon atom can only have three neighbors! It is not hard to see that every bead in the beaded ball form triangle with two near-neighbored beads. There are 60 this kind of triangles in a ball. Now we have the clue to resolve the puzzle, the beads in the beaded molecules do not correspond to the atoms, instead, they represent chemical bonds! There must be a carbon atom located at the center of each triangle. So, we can say that the beaded molecules are the bond-representation of a real molecule, instead of the commonly used atom-representation.
I made more beaded buckyballs with 4mm beads later: